Probability mass functions
library(tidyverse)
county_complete <- read_rds("county_complete.rds")Statistical distributions
During the first few weeks of the course, we learned how to use visualization for exploring a dataset and discovering trends. Now we extend this approach by bringing in concepts from probability and statistics to build a scientific foundation for interpreting these visualizations. A good starting point is with how we represent univariate (single variable) distributions, which we’ve previously visualized as frequency histograms (by default, geom_histogram() sorts data into different bins and tells you how many end up in each one). Frequency histograms are useful for examining the particulars of a single variable, but have limited utility when directly comparing distributions that contain different numbers of observations. This can occur when you group a variable into different categories or if you want to compare a variable’s distribution found in two separate experiments. We introduce two new kinds of univariate distributions that are better suited to handling these kinds of comparisons, the probability mass function (PMF), which is the subject of this part of the reading, and the cumulative distribution function (CDF), which is the subject of the subsequent reading.
Example dataset
We use an example dataset of the average time it takes for people to commute to work across 3143 counties in the United States (collected between 2006-2010) to help illustrate the meaning and uses of the probability mass function and cumulative distribution function. The frequency histogram for these times can be plotted using the following code snippet:
county_complete %>%
ggplot(mapping = aes(x = mean_work_travel)) +
geom_histogram(binwidth = 1) +
labs(title = "Average work travel times across 3143 US counties, 2006-2010",
x = "Average work travel time (min)",
y = "count")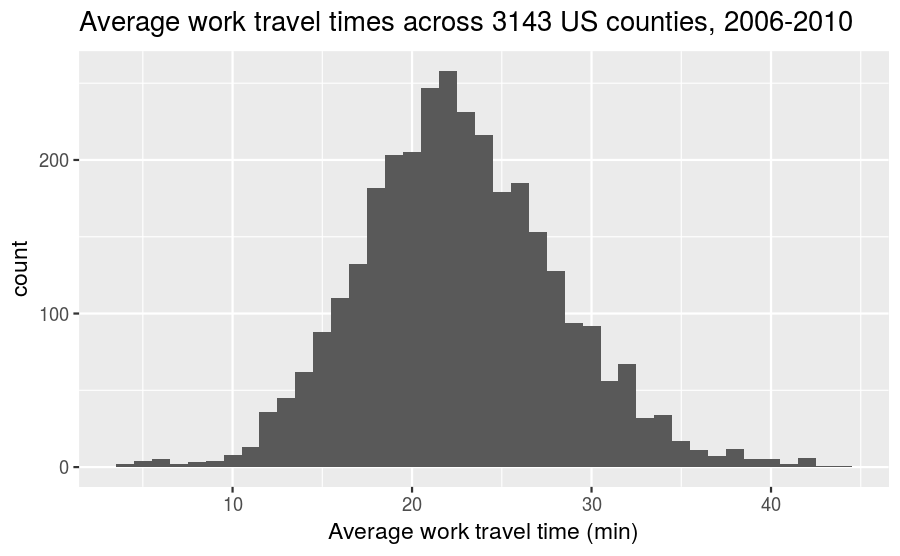
PMFs
The probability mass function (PMF) represents a distribution by sorting the data into bins (much like the frequency histogram) and then associates a probability with each bin in the distribution. A probability is a frequency expressed as a fraction of the sample size n. Therefore we can directly convert a frequency histogram to a PMF by dividing the count in each bin by the sample size n. This process is called normalization.
As an example, consider the following short sample,
1 2 2 3 5If we choose a binwidth of 1, then we get a frequency histogram that looks like this:
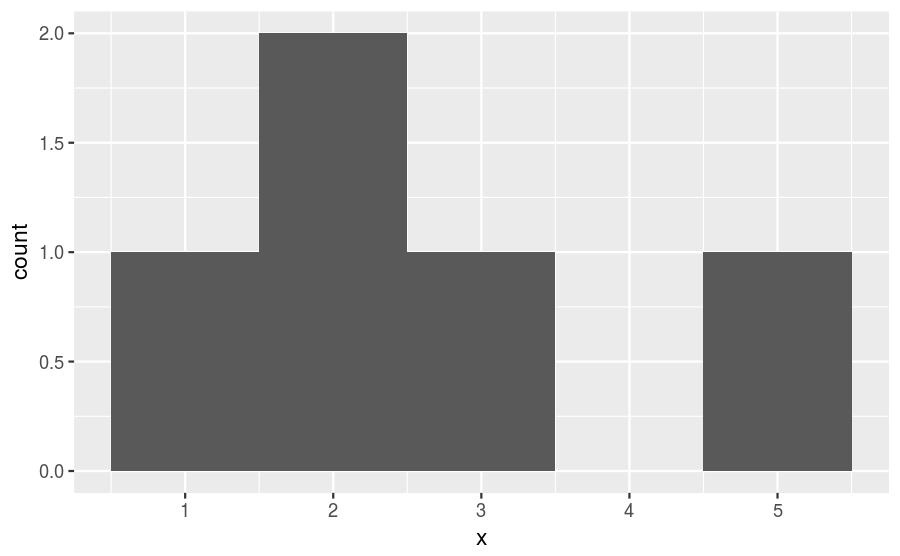
There are 5 observations in this sample. So, we can convert to a PMF by dividing the count within each bin by 5, getting a histogram that looks like this:
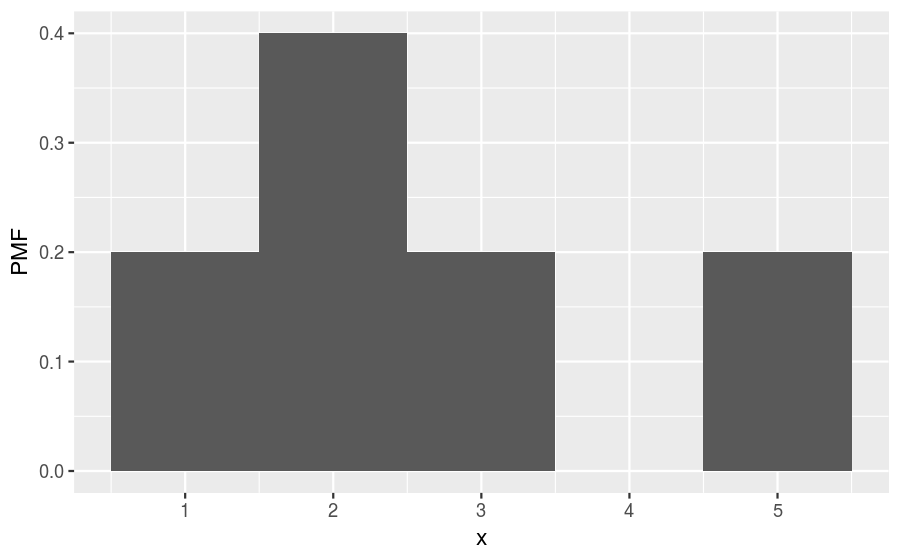
The relative shape stays the same, but compare the values along the vertical axis between the two figures. You’ll find that they are no longer integers and are instead probabilities. The normalization procedure (dividing by 5) guarantees that adding together the probabilities of all bins will equal 1. For this example, we find that the probability of drawing the number 1 is 0.2, drawing 2 is 0.4, drawing 3 is 0.2, drawing 4 is 0, and drawing 5 is 0.2. That is the biggest difference between a frequency histogram and a PMF, the frequency histogram maps from values to integer counters, while the PMF maps from values to fractional probabilities.
Plotting PMFs
The syntax for plotting a PMF using ggplot2 is nearly identical to what you would use to create a frequency histogram. The one modification is that you need to include y = ..density.. inside aes(). As a simple example, let’s take the full distribution of the average work travel times from earlier and plot it as a PMF:
county_complete %>%
ggplot(mapping = aes(x = mean_work_travel, y = ..density..)) +
geom_histogram(binwidth = 1) +
labs(title = "Average work travel times across 3143 US counties, 2006-2010",
x = "Average work travel time (min)",
y = "PMF")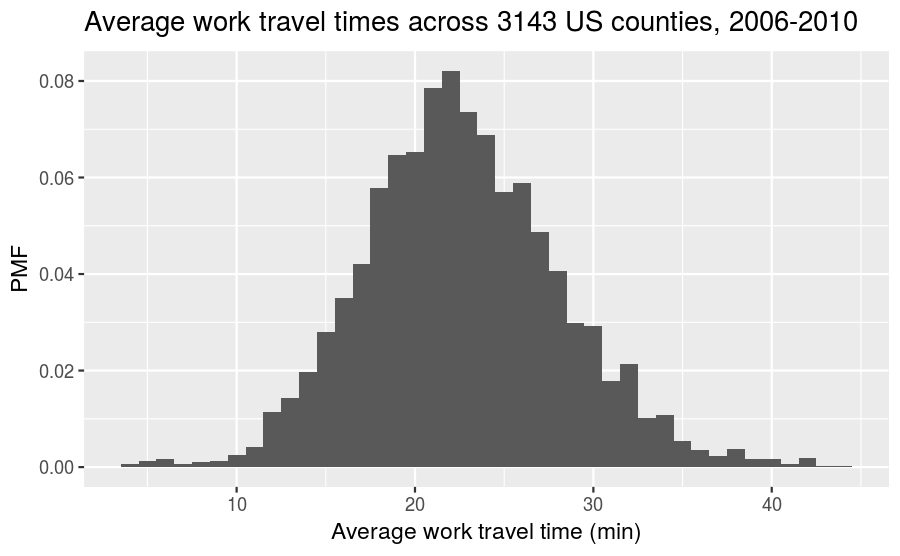
Let’s do a comparison to show how one might use a PMF for analysis. For example, we could ask if two midwestern states such as Nebraska and Iowa have the same distribution of work travel times,1 or if there is a meaningful difference between the two. First, let’s filter the dataset to only include these two states:
nebraska_iowa <- county_complete %>%
filter(state == "Iowa" | state == "Nebraska")Now let’s plot the frequency histogram:
nebraska_iowa %>%
ggplot() +
geom_histogram(mapping = aes(x = mean_work_travel, fill = state,
color = state),
position = "identity", alpha = 0.5, binwidth = 1) +
labs(title = "Average work travel times in Iowa and Nebraska",
x = "Average work travel time (min)", y = "count")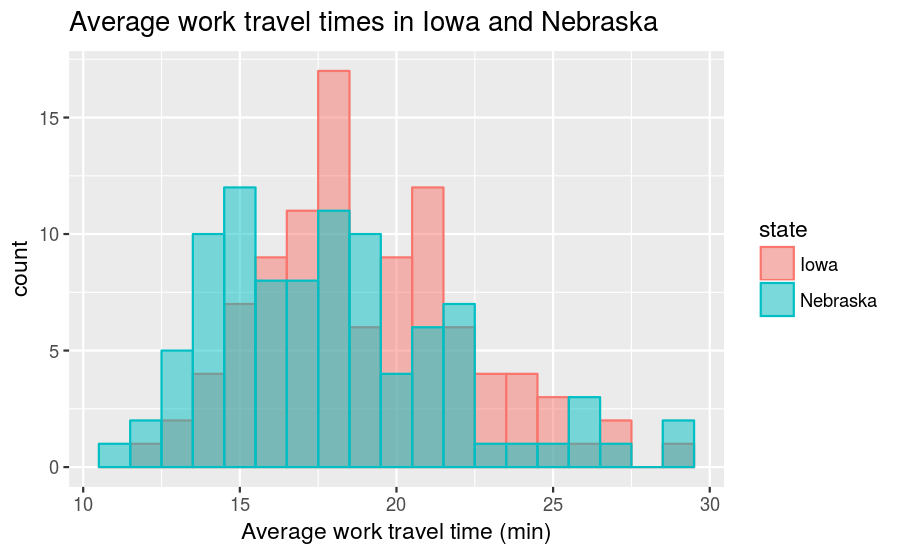
The position = "identity" input overlaps the two distributions (instead of stacking them) and alpha = 0.5 makes the distributions translucent, so that you can see both despite the overlap. On our first glance, it looks like the center of the Nebraska times is lower than the center of the Iowa times, and that both have a long tail on the right-hand side. However, if we do a count summary,
nebraska_iowa %>%
count(state)## # A tibble: 2 x 2
## state n
## <fctr> <int>
## 1 Iowa 99
## 2 Nebraska 93we find that the two states do not have the exact same number of counties, although they are close in this particular example. Nonetheless, any comparisons should be done using a PMF in order to account for differences in the sample size. We use the following code to create a PMF plot:
nebraska_iowa %>%
ggplot() +
geom_histogram(mapping = aes(x = mean_work_travel, y = ..density..,
fill = state, color = state),
position = "identity", alpha = 0.5, binwidth = 1) +
labs(title = "Average work travel times in Iowa and Nebraska",
x = "Average work travel time (min)", y = "PMF")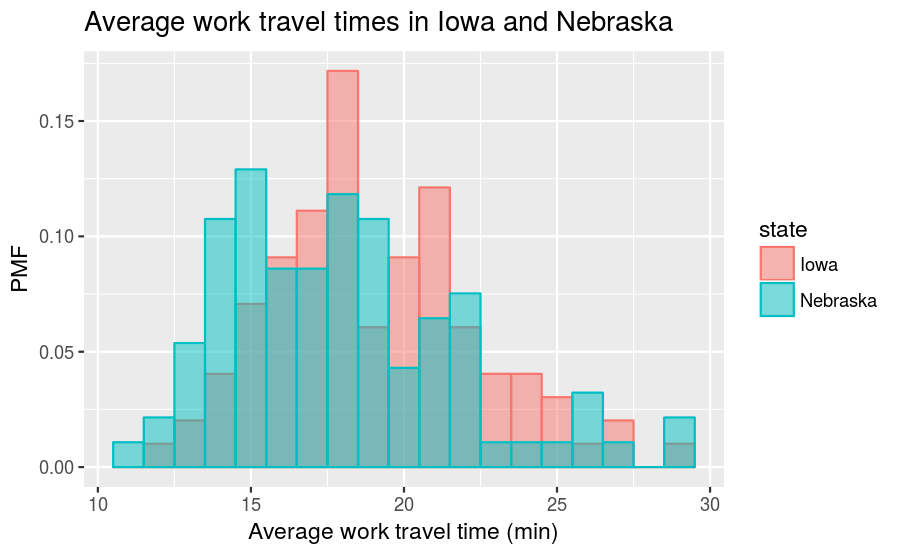
The trend that the center of the travel times in Nebraska is slightly smaller than in Iowa continues to hold even after converting to a PMF.
To provide an example where a PMF is clearly necessary, what if we compare New Jersey with Virginia? Virginia has many more counties than New Jersey:
county_complete %>%
filter(state == "New Jersey" | state == "Virginia") %>%
count(state)## # A tibble: 2 x 2
## state n
## <fctr> <int>
## 1 New Jersey 21
## 2 Virginia 134As a result, comparing their frequency histograms gives you this:
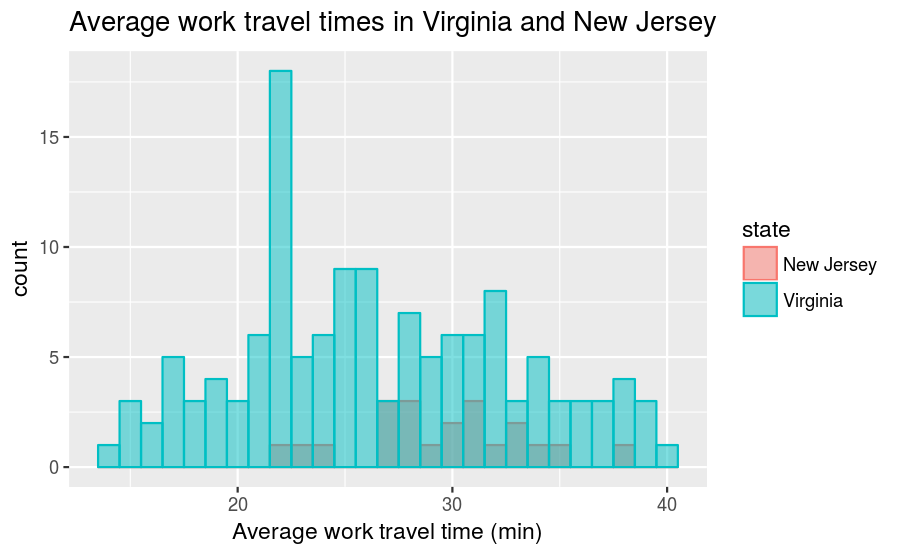
The New Jersey distribution is dwarfed by the Virginia distribution and it makes it difficult to make comparisons. However, if we instead compare PMFs, we get this:
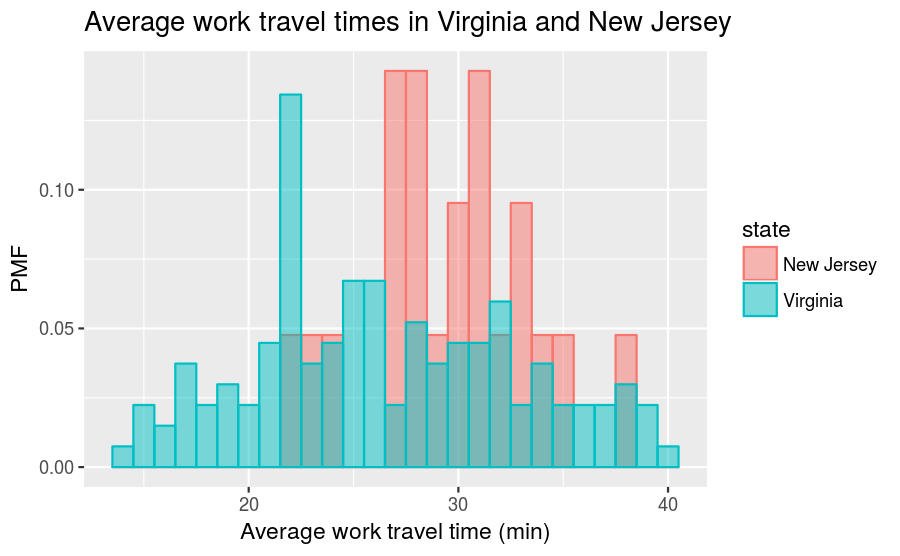
So, for example, we can now make statements like “a randomly selected resident in New Jersey is twice as likely as a randomly chosen resident in Virginia to have an average work travel time of 30 minutes.” The PMF allows for an “apples-to-apples” comparison of the average travel times.
Other visualizations
Histograms and PMFs are useful while you are exploring data and trying to identify patterns and relationships. Once you have an idea what is going on, a good next step is to design a visualization that makes the patterns you have identified as clear as possible.
In our prior comparison of the average work travel times for Nebraska and Iowa, we saw that there was a large overlap in travel times between 11 and 29 minutes, but that the overlap wasn’t exact. So it makes sense to zoom in on that part of the graph, and to transform the data to emphasize differences. To do this, we need the values of the PMF in each of the bins. The `ggplot_build() function allows us to extract these numerical values, although it takes a couple of steps to do. First, we need to create a histogram of the travel times in Iowa and Nebraska and assign it to a variable:
nebraska_iowa_histogram <- nebraska_iowa %>%
ggplot() +
geom_histogram(mapping = aes(x = mean_work_travel, fill = state),
binwidth = 1)Next, we use ggplot_build() to convert the figure into a list of information about the plot:
nebraska_iowa_figure_list <- ggplot_build(nebraska_iowa_histogram)The list has several labels containing metadata about the plot,
names(nebraska_iowa_figure_list)## [1] "data" "layout" "plot"The one that we want to use is named data. We also append [[1]] to the end, which extracts the data.frame that we want from the list. We then convert the data.frame to a tibble for convenience.
nebraska_iowa_figure_df <- nebraska_iowa_figure_list$data[[1]] %>%
as_tibble()There are 17 columns in nebraska_iowa_figure_df. Let’s use glimpse() to get a list of the variable names and previews of the first few entries:
nebraska_iowa_figure_df %>%
glimpse()## Observations: 38
## Variables: 17
## $ fill <chr> "#00BFC4", "#F8766D", "#00BFC4", "#F8766D", "#00BFC4"...
## $ y <dbl> 1, 1, 2, 3, 5, 7, 10, 14, 12, 19, 8, 17, 8, 19, 11, 2...
## $ count <dbl> 1, 0, 2, 1, 5, 2, 10, 4, 12, 7, 8, 9, 8, 11, 11, 17, ...
## $ x <dbl> 11, 11, 12, 12, 13, 13, 14, 14, 15, 15, 16, 16, 17, 1...
## $ xmin <dbl> 10.5, 10.5, 11.5, 11.5, 12.5, 12.5, 13.5, 13.5, 14.5,...
## $ xmax <dbl> 11.5, 11.5, 12.5, 12.5, 13.5, 13.5, 14.5, 14.5, 15.5,...
## $ density <dbl> 0.01075269, 0.00000000, 0.02150538, 0.01010101, 0.053...
## $ ncount <dbl> 0.08333333, 0.00000000, 0.16666667, 0.05882353, 0.416...
## $ ndensity <dbl> 7.750000, 0.000000, 15.500000, 5.823529, 38.750000, 1...
## $ PANEL <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,...
## $ group <int> 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1,...
## $ ymin <dbl> 0, 1, 0, 2, 0, 5, 0, 10, 0, 12, 0, 8, 0, 8, 0, 11, 0,...
## $ ymax <dbl> 1, 1, 2, 3, 5, 7, 10, 14, 12, 19, 8, 17, 8, 19, 11, 2...
## $ colour <lgl> NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, N...
## $ size <dbl> 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5...
## $ linetype <dbl> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,...
## $ alpha <lgl> NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, N...For our purposes, we want the x (values along horizontal axis), density (same as PMF), and group (created by fill = state) columns. We extract those using select() and then use rename() and recode() to give better names to the columns and categorical labels:
nebraska_iowa_pmf <- nebraska_iowa_figure_df %>%
select(x, density, group) %>%
rename(mean_travel_time = x, pmf = density, state = group) %>%
mutate(state = recode(state, `1` = "Iowa", `2` = "Nebraska"))With all of that work done, we can now calculate the difference in the Iowa and Nebraska PMFs. To do that, we need to spread() the state column into separate Nebraska and Iowa columns, then use mutate() to subtract the Nebraska PMF from the Iowa PMF:
nebraska_iowa_percent_difference <- nebraska_iowa_pmf %>%
spread(key = state, value = pmf) %>%
mutate(percent_difference = 100 * (Iowa - Nebraska)) %>%
select(-Iowa, -Nebraska)We remove the Iowa and Nebraska columns afterward, as we no longer need them after taking the difference. Now we can create a bar chart of the differences between Nebraska and Iowa travel times, which was the goal of this procedure:
nebraska_iowa_percent_difference %>%
ggplot() +
geom_col(mapping = aes(x = mean_travel_time, y = percent_difference)) +
labs(title = "Difference in average work travel times in Iowa and Nebraska",
x = "Average work travel time (min)", y = "Percentage points") +
coord_cartesian(xlim = c(9.5, 30), ylim = c(-7, 7)) +
annotate(geom = "segment", x = 10, xend = 10, y = 3, yend = 6,
color = "indianred3", size=0.5, alpha=1, arrow=arrow()) +
annotate(geom = "segment", x = 10, xend = 10, y = -3, yend = -6,
color = "indianred3", size=0.5, alpha=1, arrow=arrow()) +
annotate(geom = "text", x = 10, y = 6.5, label = "Iowa") +
annotate(geom = "text", x = 10, y = -6.5, label = "Nebraska")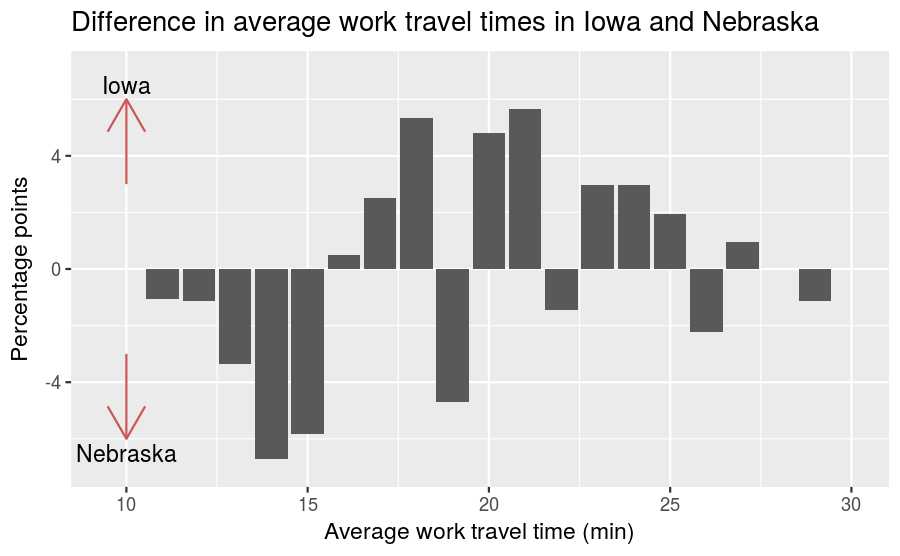
The arrows indicate that a taller bar in the \(y>0\) region means the travel time is greater in Iowa, while a taller bar in the \(y<0\) region means the travel time is greater in Nebraska. This figure makes the pattern clearer: longer work travel times are more common in Iowa than in Nebraska. For now we should hold this conclusion only tentatively. We used the same dataset to identify an apparent difference and then chose a visualization that makes the difference apparent. We can’t be sure this effect is real; it might be due to random variation. When we learn about statistical inference later on, we’ll have the tools necessary to better answer that question.
The class size paradox
Before continuing on, let’s do another PMF computation that illustrates something that we may call the “class size paradox”.
At many American colleges and universities, the student-to-faculty ratio is about 10:1. But students are often surprised to discover that their average class size is bigger than 10. There are two reasons for the discrepancy:
- Students typically take 4–5 classes per semester, but professors often teach 1 or 2.
- The number of students who enjoy a small class is small, but the number of students in a large class is (unsurprisingly) large.
The first effect is obvious, at least once it is pointed out; the second is more subtle. Let’s look at an example. Suppose that a college offers 65 classes in a given semester, with the following distribution of sizes:
| size | count |
|---|---|
| 5–9 | 8 |
| 10–14 | 8 |
| 15–19 | 14 |
| 20–24 | 4 |
| 25–29 | 6 |
| 30–34 | 12 |
| 35–39 | 8 |
| 40–44 | 3 |
| 45–49 | 2 |
If you ask the Dean for the average class size, he or she would construct a PMF, compute the mean, and report that the average class size is 23.7. Here’s the code:
class_sizes <- tribble(
~`class size`, ~count,
7, 8,
12, 8,
17, 14,
22, 4,
27, 6,
32, 12,
37, 8,
42, 3,
47, 2)
class_sizes %>%
summarize(`Average class size` = round(weighted.mean(`class size`, count), 1))## # A tibble: 1 x 1
## `Average class size`
## <dbl>
## 1 23.7But if you survey a group of students, ask them how many students are in their classes, and compute the mean, you would think the average class was bigger. Let’s see how much bigger.
First, let’s compute the distribution as observed by students, where the probability associated with each class size is “biased” by the number of students in the class. For each class size we multiply the probability by the number of students who observe that class size. The result is a new PMF that represents the biased distribution:
class_sizes2 <- class_sizes %>%
mutate(actual = count / sum(count)) %>%
mutate(observed = (actual * `class size`) / sum(actual * `class size`)) %>%
gather(key = distribution, value = PMF, actual:observed)Now we can plot the actual and observed distributions together:
class_sizes2 %>%
ggplot(mapping = aes(x = `class size`, y = PMF, fill = distribution, color = distribution)) +
geom_col(position = "identity", alpha = 0.5) +
labs(title = "Distributions of actual and observed class sizes",
x = "Class size", y = "PMF")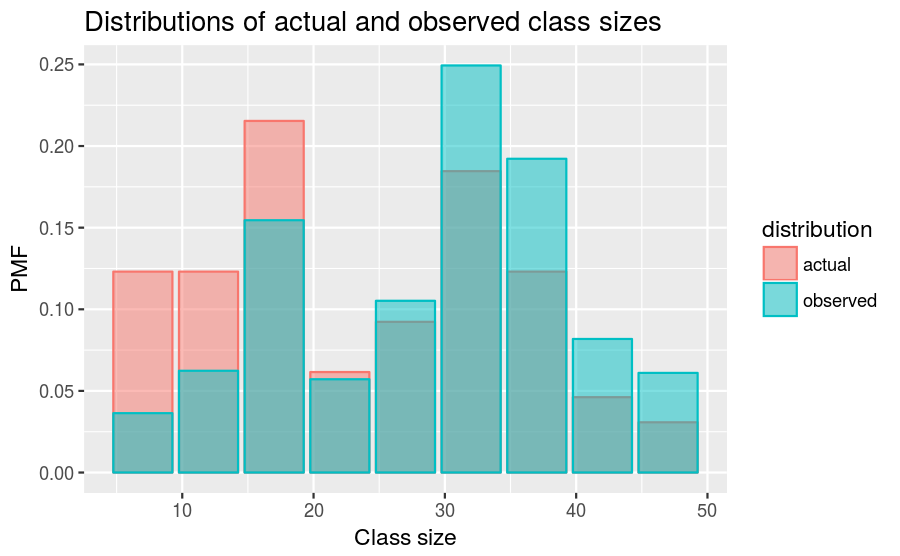
As we see in the above figure, the biased distribution corresponds to fewer small classes and more large ones. The mean of the biased distribution is,
class_sizes2 %>%
group_by(distribution) %>%
summarize(`Average class size` = round(weighted.mean(`class size`, `PMF`), 1))## # A tibble: 2 x 2
## distribution `Average class size`
## <chr> <dbl>
## 1 actual 23.7
## 2 observed 29.1which is almost 25% higher than the actual mean.
It is also possible to invert this operation. Suppose you want to find the distribution of class sizes at a college, but you can’t get reliable data from the Dean. An alternative is to choose a random sample of students and ask how many students are in their classes. The result would be biased for the reasons we’ve just seen, but you can use it to estimate the actual distribution. Here’s the code that can be used to unbias a PMF:
class_sizes2 %>%
spread(key = distribution, value = PMF) %>%
mutate(unbiased = (observed * 1 / `class size`) / sum(observed * 1 / `class size`)) %>%
select(`class size`, count, observed, unbiased, actual)## # A tibble: 9 x 5
## `class size` count observed unbiased actual
## <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 7 8 0.03636364 0.12307692 0.12307692
## 2 12 8 0.06233766 0.12307692 0.12307692
## 3 17 14 0.15454545 0.21538462 0.21538462
## 4 22 4 0.05714286 0.06153846 0.06153846
## 5 27 6 0.10519481 0.09230769 0.09230769
## 6 32 12 0.24935065 0.18461538 0.18461538
## 7 37 8 0.19220779 0.12307692 0.12307692
## 8 42 3 0.08181818 0.04615385 0.04615385
## 9 47 2 0.06103896 0.03076923 0.03076923It’s similar to before; the only difference is that it divides each probability by the class size instead of multiplying.
Credits
This work, Probability mass functions, is a derivative of Allen B. Downey, “Chapter 3 Probability mass functions” in Think Stats: Exploratory Data Analysis, 2nd ed. (O’Reilly Media, Sebastopol, CA, 2014), used under CC BY-NC-SA 4.0. Probability mass functions is licensed under CC BY-NC-SA 4.0 by James Glasbrenner.
Instructor’s note: I use Nebraska as part of this example because I received my PhD from the University of Nebraska–Lincoln. Iowa is selected for comparison due to geographic proximity.↩

